Staff profile

I am a PhD student in the Durham University Superconductivity Group, studying Time-Dependent Ginzburg-Landau (TDGL) theory through 2D/3D simulations and analytical modelling. My research focuses on the critical current density and upper critical fields in superconductors, with applications to fusion tokamaks. I hold a first class integrated master’s degree in Theoretical Physics from Durham University and am part of the EPSRC Centre for Doctoral Training in Fusion Power. 

Research Interests

The commercialisation of fusion energy as a source of energy production poses many challenges, with one of the biggest ones being the cost that comes with it. Superconductors are promising materials for the magnet systems in fusion reactors due to their ability to sustain large lossless currents to produce magnetic fields. However, observed values of the critical current density (J_c) in superconductors are found to be orders of magnitude smaller than values predicted by theoretical models [1]. 

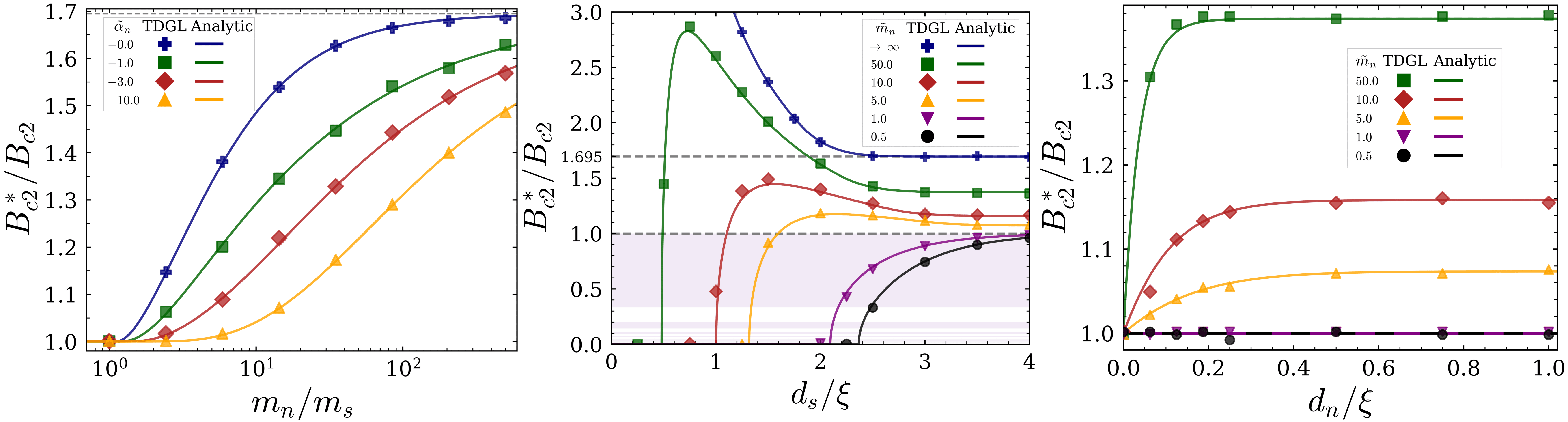
Using Time-Dependent Ginzburg–Landau (TDGL) theory, my research combines numerical simulations and analytical modelling to study the mechanisms that govern

J_c and the enhanced upper critical field (B_c2^*) in superconductors. I investigate superconducting systems with highly resistive coatings, where surface and interfacial effects lead to an enhancement in B_c2^*. By simulating 2D and 3D systems, and comparing with analytical solutions for simpler geometries, my work aims to study how these interfacial effects influence B_c2^*. Even modest improvements in these properties would significantly reduce the cost of superconductors in next-generation tokamaks. 

The systems studied range from semi-infinite superconducting–insulating (SI) and superconducting–normal (SN) interfaces to finite superconducting strips with insulating (ISI) or normal (NSN) coatings. My work also looks at SNS Josephson Junctions (JJs) and arrays of JJs. Simulations are carried out using a solver developed in the Julia programming language by Charles Haddon of the Durham University Superconductivity Group. The solver employs a non-linear geometric multigrid method to compute superconducting properties in discretised space and remains stable for arbitrary values of the Ginzburg–Landau parameter κ, unlike many other solvers that are restricted to the high-κ limit. 

Key Results

• Demonstrated that, across different geometries, the presence of a highly resistive boundary leads to an enhancement of the upper critical field (B_c2^*); 

• Observed this effect in trivial interfaces (SI, SN), coated superconducting slabs (ISI, NSN), and Josephson Junctions (SNS). In all cases, results show good agreement with existing analytical solutions [2] [3]. Systems were studied under variations in α, effective mass and system size; 

• The analytical treatment reduces the linearised second Ginzburg–Landau equation to implicit conditions expressed in terms of parabolic cylinder functions [4]. These conditions couple the applied field and the transverse wavevector k_y , where the effective upper critical field​ B_c2^* emerges as the maximum field permitting a solution. 

Future work

Future work will extend current analytic solutions for B_c2^* in flat interface systems to curved geometries, specifically cylindrical systems that better represent practical cases such as coated superconducting wires. TDGL simulations will be used to validate these results. Further directions include studying how material parameters in triple-point junctions affect the upper critical field and critical current density, as well as investigating these properties in systems with two-dimensional arrays of Josephson Junctions.  

[1] G. Wang, M. J. Raine, and D. P. Hampshire, “How Resistive Must Grain-Boundaries be to Limit Jc in Polycrystalline Superconductors?,” Supercond. Sci. Technol., vol. 30, no. 10, 2017. Art. no. 104001. 

[2] V. Ginzburg and L. Landau, “On the Theory of Superconductivity,” Zh. Eksp. Teor. Fiz., vol. 20, pp. 1064–1082, 1950. 

[3] M. Tinkham, “Effect of Fluxoid Quantization on Transitions of Superconducting Films,” Phys. Rev., vol. 129, pp. 2413–2422, 1963. 

[4] B. P. Din, “Computational and Analytic Time-Dependent Ginzburg-Landau Theory for High Resistivity High-Field Superconducting Josephson Junctions,” Doctoral, Durham University, 2024.

Left figure: Effective upper critical field at a superconducting-normal interface as a function of normal material effective mass for variable condensation parameters α_n

Right figure: Effective upper critical field in a normal-superconducting-normal (coated superconductor) system as a function of superconducting slab thickness for variable coating effective mass and a fixed condensation parameter  α_n = -3.0.